- Joined
- Mar 9, 2022
- Messages
- 16
Hi,
The last days I analysed the electricity and propellant consumption of box, triangle and manuver thruster. (No plasma, might do it some day)
And what I found out is somewhat interesting.
So, the final two functions I came up with are:
For electricity:
f(x)=d*(1e4+x*(1-c))/1e4
For propellant:
f(x)=d*(1-c/2)*(2e6/33*(1-c/2)+x*(1-c))/((2e6/33)*(1-c/2))
Well, that alone isn't that helpfull, so what each variable stands for:
x=Current thruster thrust (0 - 10000)
d=Base consumption
c=Converter efficiency in decimal (T1: 0.2, T2: 0.25, T3: 0.35)
Edit:
c Electricity: T1: 0.25, T2: 0.3, T3: 0.35
c Propellant: T1: 0.2, T2: 0.25, T3: 0.35
The function for propellant looks so complex because this converter also impacts the base consumption.
Base consumption
Through testing I fount out that each thruster has a base consumption.
The values for each thruster:
Electricity:
Box T1: 120
Box T2: 108
Box T3: 180
Triangle T1: 55
Triangle T2: 49.5
Triangle T3: 82.5
Manuver T1: 30
Manuver T2: 18
Manuver T3: 20
Propellant:
Box T1: 30
Box T2: 27
Box T3: 42
Triangle T1: 27
Triangle T2: 24.4
Triangle T3: 37.8
Manuver T1: 15
Manuver T2: 13.6
Manuver T3: 18
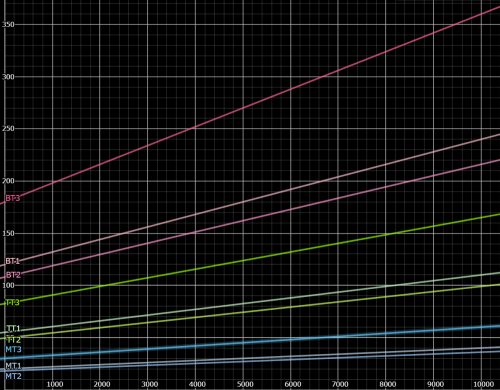
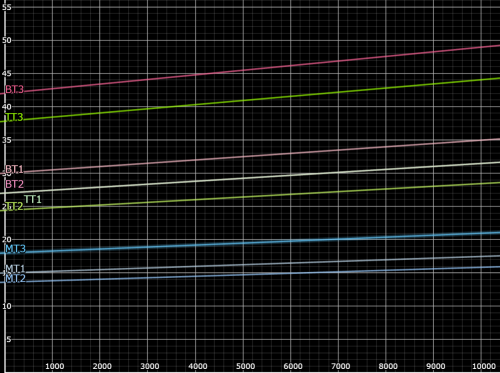
Some visualisation for each thruster
Electricity:
Propellant:
Manuver thruster
It's the same function, just without the converter influence.
For electricity:
f(x)=d*(1e4+x)/1e4
For propellant:
f(x)=d*(2e6/33+x)/(2e6/33)
Individual functions
At the beginning I reconstructed two functions for every thruster.
If somebody is interestend in those, here it is:
Electricity:
Box T1: f(x)=0.012*(1-c)*x+120
Box T2: f(x)=0.0108*(1-c)*x+108
Box T3: f(x)=0.018*(1-c)*x+180
Triangle T1: f(x)=0.0055*(1-c)*x+55
Triangle T2: f(x)=0.00495*(1-c)*x+49.5
Triangle T3: f(x)=0.00825*(1-c)*x+82.5
Manuver T1: f(x)=0.002*x+20
Manuver T2: f(x)=0.0018*x+18
Manuver T3: f(x)=0.003*x+30
Propellant:
Box T1: f(x)=0.000495*(1-c)*x+30*(1-c/2)
Box T2: f(x)=0.0004455*(1-c)*x+27*(1-c/2)
Box T3: f(x)=0.000693*(1-c)*x+42*(1-c/2)
Triangle T1: f(x)=0.0004455*(1-c)*x+27*(1-c/2)
Triangle T2: f(x)=0.0004026*(1-c)*x+24.4*(1-c/2)
Triangle T3: f(x)=0.0006237*(1-c)*x+37.8*(1-c/2)
Manuver T1: f(x)=0.0002475*x+15
Manuver T2: f(x)=0.00038*x+13.6
Manuver T3: f(x)=0.000297*x+18
When using these, keep in mind that you need to multiply then first to get rid of the decimal digits. Starbase is only working with 3 decimal digits.
For the Propellant Box T2 it's following: f(x)=(4.455*(1-c)*x+27e4*(1-c/2))/1e4 because we multiplyed it by 1000.
Propellant usage in discription
I noticed that the values in the discription are almost never correct, they are mostly close or nearby the real value. Two exceptions are manuver T3, it's the right one, and manuver T2 were the difference is 1.556. (17.4 acording to description and 15.844 in reality)
FlowId
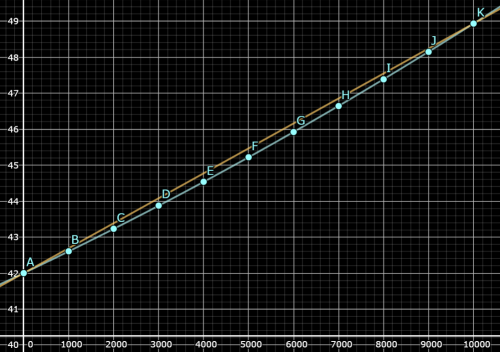
I noticed that the FlowId value is not linear, it can be found in the data field of propellant tank supports.
I think this not linear behavior is a bug, it would not make sense to use a non linear graph on somethink like that because it would mean more calulations. What is inefficient.
Graph showing the offset. The data was tested with the T3 box thruster, it consumes the most propellant.
Conclusion
The description for propellant usage should be updated to be exact.
The FlowId value is not linear for no logical reason.
And all files are in the attachment.
GeoGebra Classic was used to visualize the functions.
~ OrchideeFan944
The last days I analysed the electricity and propellant consumption of box, triangle and manuver thruster. (No plasma, might do it some day)
And what I found out is somewhat interesting.
So, the final two functions I came up with are:
For electricity:
f(x)=d*(1e4+x*(1-c))/1e4
For propellant:
f(x)=d*(1-c/2)*(2e6/33*(1-c/2)+x*(1-c))/((2e6/33)*(1-c/2))
Well, that alone isn't that helpfull, so what each variable stands for:
x=Current thruster thrust (0 - 10000)
d=Base consumption
c=Converter efficiency in decimal (T1: 0.2, T2: 0.25, T3: 0.35)
Edit:
c Electricity: T1: 0.25, T2: 0.3, T3: 0.35
c Propellant: T1: 0.2, T2: 0.25, T3: 0.35
The function for propellant looks so complex because this converter also impacts the base consumption.
Base consumption
Through testing I fount out that each thruster has a base consumption.
The values for each thruster:
Electricity:
Box T1: 120
Box T2: 108
Box T3: 180
Triangle T1: 55
Triangle T2: 49.5
Triangle T3: 82.5
Manuver T1: 30
Manuver T2: 18
Manuver T3: 20
Propellant:
Box T1: 30
Box T2: 27
Box T3: 42
Triangle T1: 27
Triangle T2: 24.4
Triangle T3: 37.8
Manuver T1: 15
Manuver T2: 13.6
Manuver T3: 18
Some visualisation for each thruster
Electricity:

Propellant:

Manuver thruster
It's the same function, just without the converter influence.
For electricity:
f(x)=d*(1e4+x)/1e4
For propellant:
f(x)=d*(2e6/33+x)/(2e6/33)
Individual functions
At the beginning I reconstructed two functions for every thruster.
If somebody is interestend in those, here it is:
Electricity:
Box T1: f(x)=0.012*(1-c)*x+120
Box T2: f(x)=0.0108*(1-c)*x+108
Box T3: f(x)=0.018*(1-c)*x+180
Triangle T1: f(x)=0.0055*(1-c)*x+55
Triangle T2: f(x)=0.00495*(1-c)*x+49.5
Triangle T3: f(x)=0.00825*(1-c)*x+82.5
Manuver T1: f(x)=0.002*x+20
Manuver T2: f(x)=0.0018*x+18
Manuver T3: f(x)=0.003*x+30
Propellant:
Box T1: f(x)=0.000495*(1-c)*x+30*(1-c/2)
Box T2: f(x)=0.0004455*(1-c)*x+27*(1-c/2)
Box T3: f(x)=0.000693*(1-c)*x+42*(1-c/2)
Triangle T1: f(x)=0.0004455*(1-c)*x+27*(1-c/2)
Triangle T2: f(x)=0.0004026*(1-c)*x+24.4*(1-c/2)
Triangle T3: f(x)=0.0006237*(1-c)*x+37.8*(1-c/2)
Manuver T1: f(x)=0.0002475*x+15
Manuver T2: f(x)=0.00038*x+13.6
Manuver T3: f(x)=0.000297*x+18
When using these, keep in mind that you need to multiply then first to get rid of the decimal digits. Starbase is only working with 3 decimal digits.
For the Propellant Box T2 it's following: f(x)=(4.455*(1-c)*x+27e4*(1-c/2))/1e4 because we multiplyed it by 1000.
Propellant usage in discription
I noticed that the values in the discription are almost never correct, they are mostly close or nearby the real value. Two exceptions are manuver T3, it's the right one, and manuver T2 were the difference is 1.556. (17.4 acording to description and 15.844 in reality)
FlowId
I noticed that the FlowId value is not linear, it can be found in the data field of propellant tank supports.
I think this not linear behavior is a bug, it would not make sense to use a non linear graph on somethink like that because it would mean more calulations. What is inefficient.
Graph showing the offset. The data was tested with the T3 box thruster, it consumes the most propellant.

Conclusion
The description for propellant usage should be updated to be exact.
The FlowId value is not linear for no logical reason.
And all files are in the attachment.
GeoGebra Classic was used to visualize the functions.
~ OrchideeFan944
Attachments
-
909.3 KB Views: 384
Last edited:
